Iga statistiline analüüs põhineb mudelil ja mudelist sõltub vähemalt sama palju kui andmetest. Erinevad mudelid, mis kasutavad täpselt samu andmeid, võivad anda miljoneid kordi erineva tulemuse – mudeli valik võib mõnikord olla sõna otseses mõttes elu ja surma küsimus.
Selle sajandi alguses vapustas Hollandit kõmuline kohtuasi. Meditsiiniõde Lucia de Berk töötas sajandivahetuse paiku kolmes Hollandi haiglas ja tema kolleegid märkasid, et just Lucia vahetuste ajal suri harilikust rohkem patsiente. Asja hakati uurima ning 2002. aastal esitati talle süüdistus 13 patsiendi mõrvas ja viie patsiendi mõrva katses.
Uurimise käigus selgus, et Lucia oli võltsinud oma õediplomit, tema päeviku sissekandeid võis tõlgendada kui kinnisideed surmast ning tema kodust leiti mitu kuulsaid mõrvu ja kohtuasju käsitlevat raamatut, mis kõik olid haiglast varastatud. Protsessi kaasati FBI kurjategijate profileerija ja kohtupsühholoog, kes kirjeldasid kohtualust kui enesekeskset, isiksushäiretega agressiivset nartsissisti.
Nende kaudsete tõendite kõrval sai kohtuasjas üheks otsustavaks teguriks matemaatika. Kohtusse kutsutud statistik tegi üsna elementaarse tõenäosusrehkenduse: ta võttis kokku kõik vaadeldava aja õdede vahetused kolmes haiglas (1734) ning võrdles neid Lucia vahetuste arvuga (201) ja nende vahetuste arvuga, mille ajal juhtusid nn intsidendid (27).
Kui suur on tõenäosus, et täiesti juhuslikult satub ühele konkreetsele meditsiiniõele vähemalt 14 surmajuhtumiga vahetust? Vastus: ligikaudu üks 3,8 miljonist. Kohus leidis, et nii väike tõenäosus välistab kokkusattumused, ning 2003. aastal mõisteti Lucia de Berk eluks ajaks vangi kui Hollandi kõigi aegade suurim sarimõrvar.
Kaheldav otsus
See kohtuprotsess tekitas ühiskonnas palju vastukaja. Pärast otsuse väljakuulutamist leidsid mitmed matemaatikud ja statistikud, et kohut veennud arvutus põhineb lihtsustatud eeldustel ega pruugi olla adekvaatne. Selle asemel et arvutada tõenäosust, et vähemat 14 intsidenti satub konkreetsele õele, oleks pidanud arvutama hoopis tõenäosuse, et vähemalt 14 intsidenti satub mingile õele; küsitavusi oli teisigi.
Üks aktiivsemaid diskuteerijaid oli Utrechti ja hiljem Leideni ülikooli statistikaprofessor Richard Gill, kes pakkus 2006. aastal koos kolleegidega välja alternatiivse analüüsi. Nad loobusid lihtsustatud eeldusest, et kõikidel õdedel on üks ja sama tõenäosus olla tööl selles vahetuses, kus juhtub intsident.
Gilli mudelis see tõenäosus varieerub, sõltudes õe haridusest, iseloomust, kogemustest ja paljust muust; suurem tõenäosus ei pruugi ilmtingimata tähendada õe ebaprofessionaalsust ega pahatahtlikkust. Seega leidsid Gill ja tema kolleegid mõnevõrra eeldusi muutes, kuid samu andmeid kasutades, et tõenäosus, et 201 vahetuse jooksul toimub vähemalt 14 intsidenti, on ligikaudu 1/49. Arvestades õdede hulka, võib selliseid olukordi elus ette tulla küll.
Suuresti just professor Gilli eestvedamisel algatati 2007. aastal petitsioon Lucia de Berki kohtuasja taasavamiseks. 2009. aastal vaadatigi lõpuks uued tõendid ja statistilised argumendid läbi ning 2010. aastal vabastati de Berk kõigist süüdistustest. Kõigi aegade suurimast sarimõrvarist sai Hollandi õigusajaloo suurima ebaõigluse ohver.
Selle pretsedendi järel hakati kogu maailmas sarnaseid kohtuasju uue pilguga vaatama. Selgus, et Lucia de Berk pole üldse ainus õde, kes on samadel alustel – suuresti matemaatiliste argumentidega – sarimõrvas süüdi mõistetud.
2023. aastal vabastati vanglast Itaalia õde Daniela Poggiali, kes oli 2014. aastal süüdi mõistetud 38 patsiendi mõrvas. Inglismaal kütab praegu kirgi Lucy Letby juhtum – tema mõisteti 2023. aastal eluks ajaks vangi süüdistatuna kümnete laste mõrvas ja mõrvakatses. Briti ühiskond on Letby süüs üsna veendunud, kuid paljud statistikud, teise seas ka Richard Gill, kahtlevad selles.
Peidetud eeldused
Igasugune statistiline analüüs, tõenäosusarvutus ning enamik prognoosi- ja tuvastusalgoritmidest põhinevad stohhastilistel ehk juhuslikkust sisaldavatel mudelitel. Seda isegi siis, kui pealtnäha mingit mudelit pole.
Toome lihtsa näite: püüame ennustada kahe võistkonna omavahelise kohtumise tulemust seniste tulemuste põhjal. Lihtsuse mõttes välistame viigi. Oletame, et seni on võistkond A võitnud 70% mängudest.
Lihtne ja pealtnäha mudelivaba mõttekäik on järgmine: A võidu tõenäosus on 0,7, see arv on suurem kui kaotuse tõenäosus (0,3), ja nii panustame A võidule. See otsus põhineb aga konkreetsel stohhastilisel mudelil, mis kätkeb eeldusi. Näiteks eeldasime, et võistkonna A võidu tõenäosus on kogu aeg sama, sest tõenäosuse 0,7 saamiseks võtsime arvesse kogu senist ajalugu.
Teine eeldus oli see, et meid huvitav tõenäosus ei sõltu seniste võitude ja kaotuste järjekorrast – me kasutasime ennustamisel vaid A võiduprotsenti andmestikus, mitte võitude ja kaotuste järjekorda. Teisisõnu eeldasime, et järgmise mängu tulemus ei sõltu eelmiste mängude tulemustest, vaid kõik algab uuesti nullist.
Nii näeme, et see pealtnäha mudelivaba ennustus põhineb tegelikult kahel väga tugeval eeldusel: sama jaotus (tõenäosus) ja sõltumatus. Erialases sõnavaras nimetatakse neid eeldusi IID-mudeliks (ingl independent and identically distributed). Paljud igapäevased tõenäosusarvutused eeldavad vaikimisi just seda, kõige levinumat statistilist mudelit.
IID-mudelile tugines suuresti ka kohtustatistik Lucia de Berki juhtumis. Lihtsusel on oma eelised, kuid nagu teame, võib liiga lihtne mudel olla eksitav. Tulles tagasi spordiennustuse juurde: on selge, et võistkondade tugevus aastate jooksul muutub, ja nii ei pruugi mõne aja tagune statistika peegeldada praegust olukorda. Hilisemat ajalugu tuleks arvestada suurema kaaluga ja see teeb mudeli keerukamaks.
Ka sõltumatuse eeldus on ebarealistlik, sest emotsioonidel on spordis suur kaal ning kord võidulainele sattunud meeskonnal on suurem tõenäosus ka järgmine kord võita. See tähendab, et järgmise matši tulemuse tõenäosus sõltub eelmiste kohtumiste tulemustest, ning seda peame oma mudelis arvesse võtma.
Sõltumatus on statistikas keskne eeldus, kuna see on intuitiivselt arusaadav ning üheselt ja lihtsalt modelleeritav. Seda eeldatakse ning kasutatakse kõikjal – pahatihti aga valesti. Sõltuvusel seevastu on palju vorme ja seetõttu on ka lõpmatult palju võimalusi seda mudelisse kaasata.
Markovi ahela peamine omadus on lihtne: homsete sündmuste tõenäosus sõltub tänasest ning eilse ega üleeilse teadmine seda ei muuda.
Ühe väga lihtsa, kuid seda universaalsema sõltuvusmudeli (juhusliku protsessi) konstrueeris 1906. aastal vene matemaatik Andrei Markov. Tänapäeval kutsutaksegi seda mudelit Markovi ahelaks. Markovi esialgne eesmärk oli näidata, et suurte arvude seadus võib kehtida ka sõltuvuse korral. Suurte arvude seadus on tõenäosusteooria ja statistika keskne printsiip, mille kohaselt läheneb aritmeetiline keskmine valimi mahu kasvades tegelikule keskväärtusele. See asjaolu on igasuguste keskmiste arvutamise teoreetiline põhjendus.
Ka spordiennustuse näites tehtud järeldus, et võistkonna võidu tõenäosus on 0,7, sest ta on siiani võitnud 70% mängudest, põhineb ainult sellel printsiibil. Enne Markovit arvati, et see printsiip kehtib vaid sõltumatuse korral, kuid oma ahelaga lükkas Markov selle eksiarvamuse ümber.
Markovi ahela peamine omadus on lihtne: homsete sündmuste tõenäosus sõltub tänasest ning eilse ega üleeilse teadmine seda ei muuda. Kaardipaki segamine, täringuvisetel põhinevad lauamängud, geneetilise koodi põlvkonniti edasikandumine – kõik need on sisuliselt Markovi ahelad. Arusaadavalt on see statistiline mudel laialt kasutusel ja matemaatiliselt põhjalikult läbi uuritud.
Oma uue mudeli eeliste näitamiseks analüüsis Markov häälikupaaride sagedusi Puškini „Jevegeni Oneginis“ ning tõestas, et häälikute modelleerimine sõltumatuna oleks kindlasti vale.
Seega võib teatud mööndustega väita, et Markovi ahelat rakendati kõigepealt keelemudelina. Nüüd, rohkem kui sada aastat hiljem, on keelemudelid igapäevased, ning lähemal uurimisel näeme, et näiteks ChatGPT polegi muud kui (väga kõrget järku) Markovi ahel.
Varjatud mudelid
Sageli on vaja modelleerida olukordi, kus Markovi ahelat ei saa täpselt mõõta – näiteks patsiendi tervisliku seisundi hindamisel.
Seisundeid võib olla kaks: haige või terve. Haigust me mõõta ei saa, küll aga selle tunnuseid: temperatuuri, vererõhku jne. Mõõdetavad tunnused ei pruugi üheselt näidata olekut (ka terve inimese vererõhk võib vahel olla normist väljas), küll aga on tunnuste jaotus tervel ja haigel inimesel erinev.
Eeldades, et mõõdetavad tunnused on tinglikult sõltumatud, jõuame ülipopulaarse mudelini, mida nimetatakse varjatud Markovi mudeliks. Selle edulugu algas 1980-ndatel seoses kõnetuvastusega, kui kõne (nii keel kui ka foneetika) modelleeriti kui üks suur varjatud Markovi mudel, millel on sadu tuhandeid parameetreid.
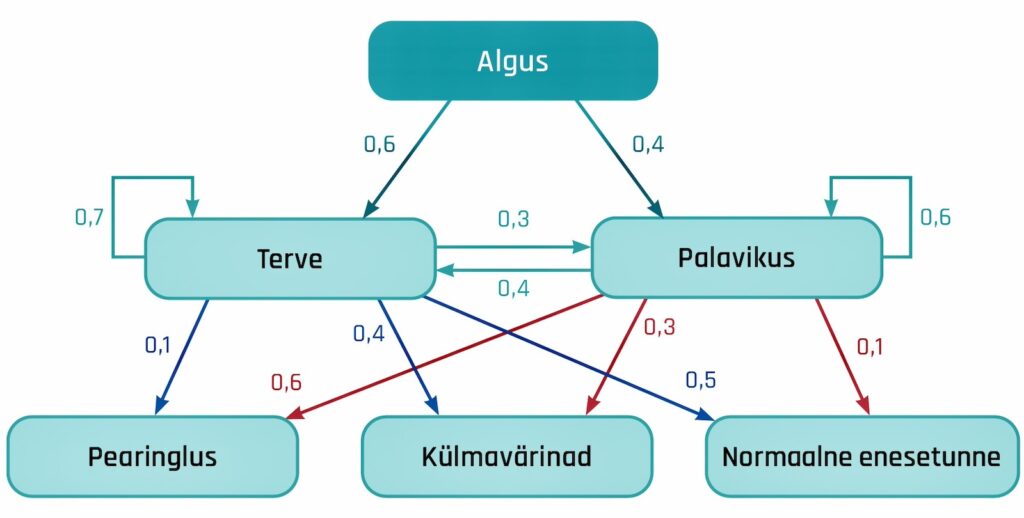
Varjatud Markovi mudelid (ahelad) kuuluvad varjatud ehk latentsete tunnustega mudelite hulka, kus eeldatakse, et vaatlused (ehk mõõdetav maailm) on tekitatud mingi mõõdetamatu (seega varjatud), kuid olulise protsessi tulemusena.
Siin tekib loomulik küsimus: milline varjatud protsess (stsenaarium) tekitab vaatlused? Kas ülaltoodud näite korral tähendavad normist väljas olevad tervisenäitajad ikka haigust? Kui jah, siis millal see algas?
Me võime arvutada iga võimaliku stsenaariumi tõenäosuse, kuid me ei saa kunagi teada, milline neist tegelikult realiseerub. Küll aga saame välja valida stsenaariumi, mis meie hinnangul peegeldab parimal moel tegelikult toimunut – enamasti valitakse selleks kõige tõenäolisem stsenaarium.
Varjatud Markovi ahelate kontekstis nimetatakse kõige tõepärasemat stsenaariumi Viterbi teeks (sest algoritmi sellise tee leidmiseks nimetatakse selle looja Andrew Viterbi järgi Viterbi algoritmiks). Matemaatiliselt on Viterbi algoritm erakordselt lihtne nn dünaamilise planeerimise algoritm, mis ometigi tegi selle loojast kuulsa ja rikka mehe. Lihtsus loeb!
See populaarne algoritm annab kasutajale suurima tõepäraga stsenaariumi, kuid edasine sõltub sellest, mida saadud Viterbi teega peale hakata. Tuleb meeles pidada, et Viterbi teed ei maksa võtta tegeliku stsenaariumina – see on tõenäosuse mõttes parim, aga parim pole kunagi tüüpiline.
Kujutagem ette mündiviset, kus kulli tõenäosus on 0,7. Visates seda münti n korda, saame suure tõenäosusega jada, kus on suurte arvude seaduse järgi ligi 70% kulle. Kõikvõimalikest viskestsenaariumidest on selle mündi puhul suurima tõenäosusega jada, kus on ainult kullid. Selline jada (meie näite Viterbi tee) on aga väga ebatüüpiline, sest tõenäoliselt peaks sinna sattuma vähemalt mõni kiri.
Paraku pole keerulisemate mudelite korral üldse selge, kas Viterbi tee mingeid omadusi põhjustab juhus või on kõige taga mingi süsteemsus. Süsteemsuse kindlakstegemine on keeruline matemaatiline probleem, mille uurimisega me koos toonase kolleegi Alexey A. Koloydenkoga üle 20 aasta tagasi algust tegime.
Töötasime sel ajal mõlemad järeldoktorandina ühes Hollandis asuvas rahvusvahelises instituudis. Uurima ajendas meid toonaste kõnetuvastusprogrammide treeningalgoritmide analüüs. Esimese sammuna tõestasime Viterbi protsessi olemasolu.
Viterbi protsess ei pruugi alati olemas olla, kuid kui ta on, siis on ta hädavajalik matemaatiline töövahend Viterbi tee süstemaatiliste omaduste kindlakstegemiseks. Selle kaudu saab kindlalt väita, et süstemaatilised omadused on olemas, ja see on tegelikult juba suur samm edasi.
Et sellest teadmisest kasu lõigata, tuleb aru saada, kuidas need omadused mõjutavad Viterbi tee põhjal tehtud järeldusi. See ei ole lihtne, kuid lahendustel on suur praktiline tähtsus, sest nii on võimalik näiteks andmeteadlasele öelda, mida võib ja mida ei tohi Viterbi teest järeldada. Mündiviske näites ei tohi Viterbi teest järeldada, et kulli tõenäosus on 1, küll aga saab järeldada, et see on vähemalt 0,5.
Ohtlik lihtsustamine
Varjatud Markovi ahel on küll lihtne mudel, mida kasutatakse palju, kuid see jääb mingites olukordades paraku liiga primitiivseks. See mudel eeldab, et mingi kindla varjatud tunnustega stsenaariumi korral on vaatlused sõltumatud. Tihti pole see aga nii, ja nagu kohtualustest õdede juhtumid näitasid, võib mudeli ülelihtsustamine olla saatuslik.
Samas põhinevad Viterbi ja teised olulised algoritmid just Markovi ahela omadusel ega tööta ilma selleta. Varjatud Markovi ahelat on aga võimalik üsna palju üldistada, kaotamata siiski vajalikku omadust.
Niinimetatud paarikaupa Markovi mudel koosneb kahest juhuslikust protsessist (vaatlused ja varjatud stsenaarium), millest kumbki eraldi ei pruugi olla Markovi ahel, kuid kahepeale kokku on nad seda küll. Ja algoritmid (neid tuleb küll natuke kohendada) töötavad ikka.
Erinevalt varjatud Markovi ahelatest on üldisemad paarikaupa mudelid suhteliselt vähetuntud ja neid pole ka eriti süstemaatiliselt uuritud. Seda viga püüame Tartu Ülikoolis minu juhitavas juhuslike protsesside töörühmas parandada. Matemaatiliselt on sellised mudelid paraku märksa keerukamad. Siiski õnnestus Joonas Soval oma doktoritöös konstrueerida hädavajalik tööriist – Viterbi protsess, mis võimaldab üldistada mitmeid seni vaid varjatud Markovi mudelite korral tõestatud teoreeme.
Meie töörühma sõnum andmeteadlasele on lihtne: kui leiad, et varjatud Markovi ahel on piisavalt realistlik, siis kasuta seda, sest lihtsus loeb. Kui aga leiad, et eeldused pole täidetud, siis ole teadlik sellest, et on ka palju teisi ja mitmeski mõttes reaalsusele lähedasemaid mudeleid.
Paljukasutatud Viterbi tees võib olla keskmiselt liiga palju dekodeerimisvigu, kuid nii varjatud kui ka paarikaupa Markovi ahelate korral on suhteliselt lihtne leida minimaalse keskmise vigade arvuga täpseim tee. Paraku võib selle tõenäosus olla väga väike, isegi null.
Sellist lahendust on praktikutel raske aktsepteerida – parim stsenaarium ei saa ju ometi olla võimatu! Probleemile, et parim tee vigade arvu mõttes võib olla halvim tõenäosuse mõttes, juhtis juba 1980-ndatel tähelepanu statistilise kõnetuvastuse rajaja Lawrence Rabiner. Tema pakutud väljapääs oli optimeerida olekupaaride tõenäosuste summat – see ei anna küll vigade mõttes parimat tulemust, kuid midagi sinna kanti. Paraku ei ole see lahendus, sest ka maksimaalses summas võib mõni liidetav ikka olla null (ja nii on ka kogu tee tõenäosus null).
Pakkusime koos Koloydenkoga välja algoritmi, kus summa asemel maksimeeritakse korrutist. Korrutis saab olla nullist erinev vaid siis, kui ükski tegur pole null. Seda ideed edasi arendades jõudsime nn hübriidalgoritmide klassini.
Selle tulem on nn hübriidtee, mis ühendab head omadused: suhteliselt vähe vigu ja suhteliselt suur tõenäosus. Algoritmi on kerge üldistada paarikaupa Markovi mudelitele ning praegu käib töö algoritmi eeliste tutvustamiseks konkreetsete rakenduste kaudu. Teeme selles vallas koostööd Aarhusi Ülikooli professori Asger Hobolthiga, kelle uurimisrühm on saanud viimasel ajal hübriidalgoritmide rakendamisel paljutõotavaid tulemusi.











Lisa kommentaar